NanoLogic Setlogic

SETLOGIC

next>

The meaning of SETLOGIC
Setlogic means the representation and manipulation of a set of data as single entities. Like topologic, the consequences of implementing setlogic in computing will have profound and probably revolutionary effects. NanoLogic has developed a procedure, based on topologic, for designing circuits to represent any expression in Set Theory and perform computations with them.


Computational Set Theory

Set Theory is the fundamental formalism upon which all mathematics is based. It provides a unified approach to defining mathematical objects and procedures for manipulating those objects. “Computational set theory” is that branch of set theory concerned with manipulating set expressions to achieve a particular purpose, e.g., to obtain “solution” sets representing unknowns in the problem. This program involves operations such as combining given sets to form new sets, testing relationships between sets, etc.

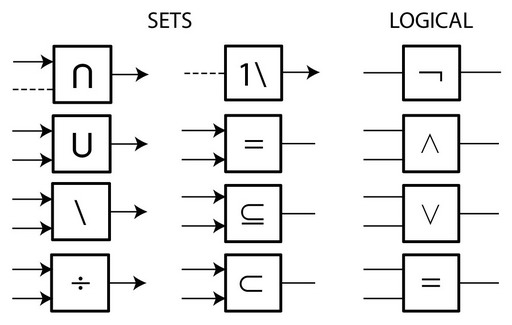
Set Theory uses a small number of canonical expressions for defining and combining sets to form other sets, and for expressing any mathematical idea. The language is generally defined with the following canonical elements:

Using these expressions, we can construct any expression in Set Theory, and therefore any mathematical expression.

NanoLogic's circuit design strategy

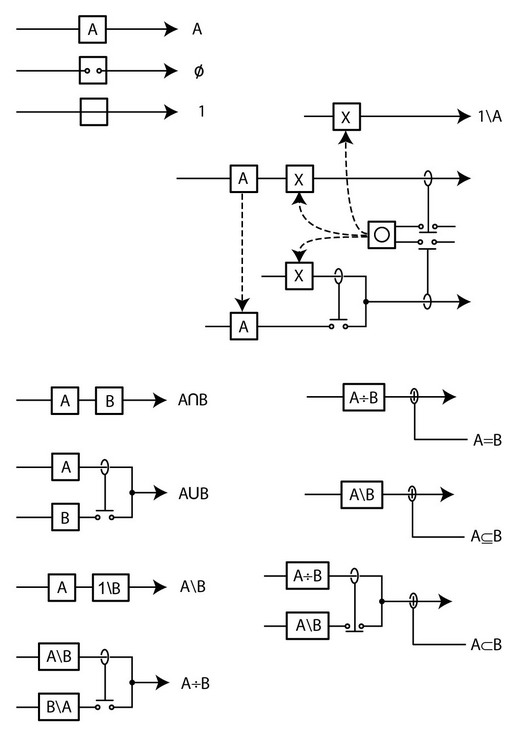
In the topologic idiom, we have developed simple canonical circuits that are analogues of the core expressions in Set Theory. In current mode, they are:

There is an entirely equivalent set of voltage-mode circuits. These circuits can be written in a convenient form in which there is 1 or 2 inputs and 1 output, viz:

With these, it is a simple matter to assemble the complete circuit analogue of any Set Theory expression. An example of such a circuit, used to solve a traditionally intractable problem, is given next.

Example: Circuit analogues of arbitrary expressions
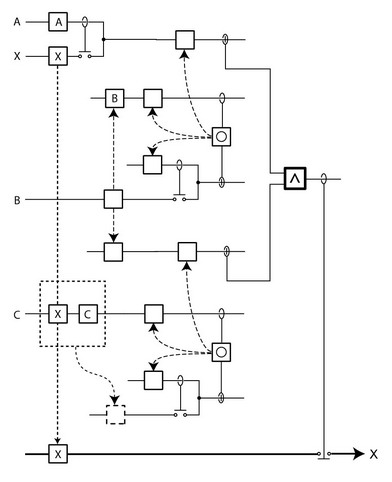
Expressions in Set Theory are of two types: they can generate new sets from given sets, and they can specify constraints between the sets. Here is a simple, but typical, pair of constraints between four sets:

Using the table of circuit fragments given above, it is easy to assemble a complete circuit that is the analogue of this set of constraints:



Example: The intractable problem of set splitting
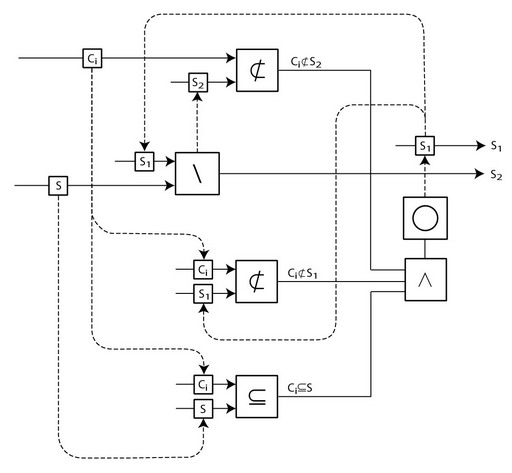
As an example of the use of setlogic, we examine a classic intractable problem: Set Splitting [M. R. Garey and D. S. Johnson, Computers and intractability: A Guide to the theory of NP-completeness, W. H. Freeman, San Francisco (1979).]

[SP4] SET SPLITTING
INSTANCE: Collection C of finite subsets of a finite set S.
QUESTION: Is there a partition of S into two subsets S₁ and S₂ such that no subset in C is entirely contained in S₁ or S₂?

The following circuit can be drawing very easily by simply requiring all the conditions implied by the statement of the problem.

Not only will this circuit solve the original intractable problem, which assumes the sets are finite, but it is valid for infinite sets (continuous functions) as well. Thus, the setlogic approach provides a significant extension of the capability to evaluate intractable problems, i.e., to infinite sets.


The importance of setlogic

In a sense, setlogic is essentially parallel data manipulation. That is, given a set of values, a conventional (Von Neuman) computer would process one value at a time, in sequence. This is equivalent to printing a half-tone picture one dot at a time. Obviously it is far more efficient to print the entire picture in one operation, and this is made possible by folding the space from a linear dot sequence into a 2D array and performing operations on all points in the array simultaneously.

In setlogic, we envision representing the entire set of values by individual devices or circuits, and performing set-level operations on all values simultaneously. This is made possible by connecting and disconnecting the devices and circuits in such a way that the fundamental operations in Set Theory are satisfied. For instance, connecting two devices in series produces a (compound equivalent) device that is the analogue of the intersection of the two individual device sets. This is a far more efficient process than computing the intersection value-by-value.

The importance of setlogic in the next generation of topologic-based computers cannot be overstated. The ability to manipulate functions rather than values will lead to significantly new algorithms and standards for computational efficiency.