|
|
- The meaning of TOPOLOGIC
Topologic means that the computer used to represent (simulate) a complex system has the same topology as the system itself. The consequences of this principle are profound and probably revolutionary. NanoLogic has developed a procedure for designing circuits according to this principle.
- The fundamental principle of simulation is that the more closely a simulating system resembles the physical system, the more efficient (=fast) it will be. For instance, for many aspects of interest, a cup of water is an extremely efficient simulator of a cup of coffee. In contrast, a digital computer, which has no physical relation to a cup of coffee, is extremely inefficient (and slow).
- In seeking a more efficient computational paradigm for 21st-Century problems, we realized that many, if not most, of the really important problems are considered "hard" because historically we have attempted to solve them with digital computers. The data representation in such computers is too detailed (bits), and there are too many pieces of data (e.g., petabits). For such problems we neither have enough input data nor do we want such detailed output data. Rather, we often (usually) have a general description for input, and we only want an general description for output. But this is precisely what topology provides us: a general description of the gross features (e.g., connectivity) of classes of systems, with no details about any specific system. While we might decry the loss of detail, we can revel in the fact that by working with a topological class rather than a specific system we might actually be able to solve problems considered intractable for digital computers. We believe that this is the future of computing, namely topological data, system-specific circuits, and analog signals.
- NanoLogic's design strategy
- NanoLogic has codified the topologic concept in the following design procedure:
- 1. Resolve the system into a (relatively small) set of canonical pieces, from which the system, and any other system in the topological class, can be constructed by simply joining the pieces.
- 2. Design a canonical set of (relatively simple) circuits that are analogues of the system pieces, in the sense that the functioning of the circuits is acceptably similar to the functioning of the analogue piece in the system.
- 3. Assemble a complete circuit by joining the circuit pieces into the same topology as the physical system.
The complete circuit so assembled is guaranteed to be a faithful analogue of the complete physical system, because every piece of it is a faithful analogue of the corresponding piece of the system (linear superposition). The complete circuit is exercised by varying its parameters in a manner that corresponds to the desired parametric variation in the physical system. Note that the data in such a system is not numbers--it is an analog computer. It is fair to refer to such as machine as a computer, because it represents and manipulates electrical signals in such a manner that they correspond to meaningful transformations in the physical system.
- Application: Chaotic dynamics
- We show here how topologic can be applied to a model physical system: topological chaotic dynamics.
- From the work of Gilmore and others [R. Gilmore and M. Lefranc, The Topology of Chaos: Alice in Stretch and Squeezeland, Wiley (2002).], chaotic systems have been very successfully described with topological models, using a structure called branched manifold. A branched manifold is a multi-branched and multiply-connected ribbon structure. The state of the system is represented as a point that moves around the branched manifold. Within a range of control parameters, it is possible to cause the system point to move on a multi-periodic or aperiodic (chaotic) trajectory. Our goal is to be able to devise a circuit that is a physical analogue of any arbitrary branched manifold.
- Here is a typical branched manifold:
- The first step is to idealize this structure, thus:
- The branched manifold is further idealized by restricting bends, turns, and rotations to 90o:
- Essentially any such idealized branched manifold can be assembled from the following canonical pieces:
- We have designed a set of simple circuits that are analogues of the ideal pieces:
-
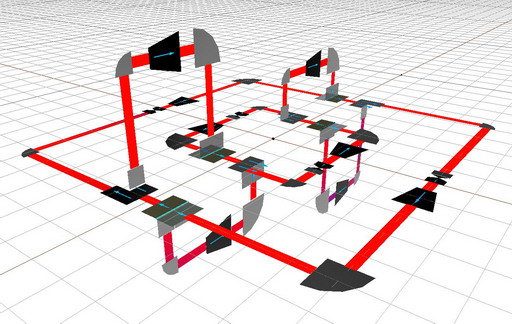
- We can use these circuit fragments to assemble a complete circuit with the same topology as the original branched manifold. The circuit fragments are joined end-to-end with the same connectivity as the branched manifold. Here is the beginning of the assembly:
The complete circuit is easily assembled. That the circuit is the topological equivalent of the branched manifold is obvious.
- The complete circuit is guaranteed to be a faithful analogue of the complete physical system, hence its behavior as circuit parameters are varied will be a faithful representation of the behavior of the chaotic system, to within the accuracy of the topological model.
Dynamic topology
This example is based on fixed topology of the branched manifold, and of its analogue circuit. However, if the control parameters in a chaotic system are altered significantly, the attractor and its idealized branched manifold can be changed--new branches generated, others merged. Such violent changes are well within the topologic paradigm, since the circuit is easily made to be adaptive: if its behavior satisfies any of a set of criteria, the circuit is modified by analog switches.
|